このwikiの更新情報RSSヤングの干渉実験（理論）
ダブルスリットの干渉条件とともに，シングルスリットによる回折干渉の条件を整理する。
1.ヤングの干渉条件
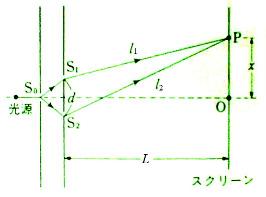
一般に光路差は次のように求められる。
この近似計算は，回折格子の光路差の近似を流用した方が見通しがよくて簡明である。すなわち，
したがって，明線条件は
明線間隔は，
となる。
明線間隔は，
となる。
2.単スリットによる干渉
回折による干渉は，単スリットによっても起こることが知られている。
スリット中央の幅
の部分から点Pに届く光波の関数を
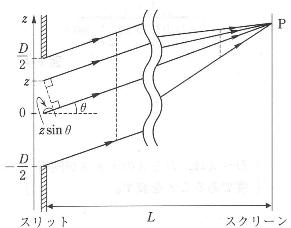
スリット中央の幅
の部分から点Pに届く光波の関数を
とすると，位置 
の幅 の部分から届く光波は，
の幅 の部分から届く光波は，
となる。点Pで観測される光波は,
これを積分して
これを積分して
となる。したがって，観測される明るさは 
の明るさを
として
の明るさをとして
と書ける。この結果は２つの事実を示している。すなわち，
(1) 実質的な回折角 
が 
となること。
(2)
を間隔として弱い干渉縞が現れること。
が となること。
(2)
を間隔として弱い干渉縞が現れること。
である。
ちなみに，この幅
をもつ間隔 
のダブルスリットでヤングの干渉実験をおこなうと，明線間隔 
の干渉縞が間隔 
を周期とする単スリット回折による変調をともなっていることが観察される。
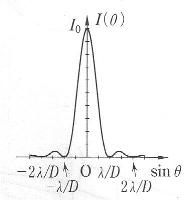
ちなみに，この幅
をもつ間隔 のダブルスリットでヤングの干渉実験をおこなうと，明線間隔 の干渉縞が間隔 を周期とする単スリット回折による変調をともなっていることが観察される。
参考文献
(1) 吉田弘幸著 SEGハイレベル物理VOL.4「光波・原子」（1998 SEG出版）
(2) 啓林館ユーザーの広場
(2) 啓林館ユーザーの広場
(2008.12.17)
