複素数引数ベッセル関数の実装 - 超音波流体屋のプログラム備忘録

(2015/03/27編集, 前の関数は遠方で発散するので)
cuda上で複素数入力のハンケル関数(complex Bessel function, Hankel function)を扱いたかったんでメモ。
四角い車輪の再発明なので用途に困ったとき以外は素直にboostライブラリの関数や、fortranライブラリの流用を検討すること。

complex_bessel : GitHub
scipy.special.hankel2 : SciPy
Cyclic Hankel Functions : boost.org
amos : http://www.netlib.org/amos/

計算式

$\L J_n(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m!(n+m)!} \left( \frac{z}{2} \right)^{2m+n} $
$\L Y_n(z) = \frac{2}{\pi} J_n(z) \ln\frac{z}{2} - \frac{1}{\pi} \sum_{m=0}^{n-1} \frac{(n-m-1)!}{m!} \left( \frac{z}{2} \right)^{2m-n} -\frac{1}{\pi} \sum_{m=0}^{\infty} \frac{\psi(m+1)+\psi(n+m+1)}{m!(n+m)!} (-1)^m \left( \frac{z}{2} \right)^{2m+n} $
$\L \psi(m) = -\gamma - \frac{1}{m} + m \sum_{i=1}^\infty \frac{1}{i(i+m)} $
(γ=0.5772...はオイラー数)

遠方でハンケル関数は以下なので、上の計算オーダーをm=25までとして、abs(z)=5πで切り分ける。
$\L H_n(|z|\gg 1) \simeq \sqrt{\frac{2}{\pi z}} \exp\left[-j\left(z-\frac{n\pi}{2}-\frac{\pi}{4}\right)\right]$

オイラー数とψ(polygamma)関数の処理をまともにやると手間食うので厳密値をもらっておく。polygamma関数の厳密値
十分入力が大きくなれば近似で十分なので、Series polygamma(x)
x=20における近似誤差=1.6e-13なのでたぶん問題ないはず。

参考
[1] (pdf)特殊関数とその応用について - 自然系教育講座 - 兵庫教育大学
[2] (pdf)Bessel 関数の数値計算
[3] DLMF : Hankel Functions
[4] GSL - GNU Scientific Library

関数本体

CUDA上で使用したかったので、thrustの複素数ルーチンを使用する。
cuComplexでやりたければ、typedefの行とオペレーターとpowとexpが複素数非対応なのに注意して実装する。

#include <stdio.h>
#define _USE_MATH_DEFINES
#include <math.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <thrust/complex.h>
typedef thrust::complex<double> zcmplx;
 
#define GAMMA 0.57721566490153286060651209008240
#define PSIMAXORD 20
 
#define TLR2EXP (5*M_PI)
#define ORD 25
 
double factorial(int n) { return tgamma(n + 1); }
double psi(int n)
{
 
	double res;
	double gam[PSIMAXORD] = {
		0.0, 1.0, 3.0 / 2.0, 11.0 / 6.0, 25.0 / 12.0,
		137.0 / 60.0, 49.0 / 20.0, 363.0 / 140.0, 761.0 / 280.0, 
		7129.0 / 2520.0, 7381.0 / 2520.0, 
		83711.0 / 27720.0, 86021.0 / 27720.0, 
		1145993.0 / 360360.0, 1171733.0 / 360360.0,	1195757.0 / 360360.0,
		2436559.0 / 720720.0, 42142223.0 / 12252240.0,
		14274301.0 / 4084080.0, 275295799.0 / 77597520.0};
 
	if (n < 1) res = 0.0;
	else if (n <= PSIMAXORD) res = gam[n - 1] - GAMMA;
	else
	{
		res = -1.0 / (252.0*pow(n, 6)) + 1.0 / (120.0*pow(n, 4)) - 1.0 / (12.0*pow(n, 2));
		res += -1.0 / (2.0*n) - log(1.0 / n);
	}
	return res;
}
 
zcmplx hankel(int n, zcmplx z)
{
	zcmplx hres = zcmplx(0, 0);
	if (abs(z) < TLR2EXP)
	{
		zcmplx jres = zcmplx(0, 0);
		zcmplx yres = zcmplx(0, 0);
		for (int m = 0; m <= n - 1; m++)
		{
			double ycoeffB = 1.0 / M_PI * factorial(n - m - 1) / factorial(m);
			yres -= ycoeffB* pow(z / 2.0, 2.0 * m - n);
		}
 
		zcmplx ycoeff1 = 2.0 / M_PI*log(z / 2.0);
		for (int m = 0; m <= ORD; m++)
		{
			zcmplx jnume = pow(-1.0, m) * pow(z / 2.0, 2.0 * m + n);
			double jdeno = factorial(m)*factorial(n + m);
			jres += jnume / jdeno;
 
			zcmplx ytermA = ycoeff1*(jnume / jdeno);
			double ynumeC = psi(m + 1) + psi(n + m + 1);
			zcmplx ytermC = (ynumeC / jdeno / M_PI)*jnume;
			yres += (ytermA - ytermC);
		}
		hres = jres + zcmplx(0, -1)*yres;
	}
	else
	{
		zcmplx ares = sqrt(2.0 / (M_PI*z));
		zcmplx pres = zcmplx(0, -1)*(z - n*M_PI / 2.0 - M_PI / 4.0);
 
		hres = ares * exp(pres);
	}
 
	return hres;
}
 
#define CYC 10
#define DIV 40
 
int main()
{
	FILE *f;
	double dx = M_PI / DIV;
	zcmplx ks = sqrt(1.0 / zcmplx(0,1));
	f = fopen("res.dat", "w");
	for (int i = 1; i <= CYC*DIV; i++)
	{
		double x = i*dx;
		zcmplx y = ks*x;
		zcmplx h0_x = hankel(0, x);
		zcmplx h1_x = hankel(1, x);
		zcmplx h0_y = hankel(0, y);
		zcmplx h1_y = hankel(1, y);
 
		fprintf(f, "%e, %e %e %e %e %e %e %e %e\n", x,
			h0_x.real(), h0_x.imag(), h1_x.real(), h1_x.imag(),
			h0_y.real(), h0_y.imag(), h1_y.real(), h1_y.imag());
	}
	fclose(f);
    return 0;
}
 

精度検証用Matlabプログラム

5π=15.7なのでその辺を目視で確認したり。

clear;
j=1i;
 
load res.dat;
x=res(:,1);
X0=res(:,2)+j*res(:,3);
X1=res(:,4)+j*res(:,5);
Y0=res(:,6)+j*res(:,7);
Y1=res(:,8)+j*res(:,9);
 
ks=sqrt(1/j);
y=ks*x;
 
x0=besselh(0,2,x);
x1=besselh(1,2,x);
y0=besselh(0,2,y);
y1=besselh(1,2,y);
 
plot(x, real(x0), x, real(X0), 'o', x, imag(x0), x, imag(X0), 'o');  xlim([15 20]);
plot(x, real(x1), x, real(X1), 'o', x, imag(x1), x, imag(X1), 'o');  xlim([15 20]);
plot(x, real(y0), x, real(Y0), 'o', x, imag(y0), x, imag(Y0), 'o'); ylim([-1e-5 1e-5]);
plot(x, real(y1), x, real(Y1), 'o', x, imag(y1), x, imag(Y1), 'o');  ylim([-1e-5 1e-5]);
 
ex0 = abs(x0-X0); semilogy(x, ex0);
ex1 = abs(x1-X1); semilogy(x, ex1);
ey0 = abs(y0-Y0); semilogy(x, ey0);
ey1 = abs(y1-Y1); semilogy(x, ey1);
 
plot(x, real(x0), x, real(X0), '.', x, imag(x0), x, imag(X0), '.',...
 x, real(y0), x, real(Y0), '.', x, imag(y0), x, imag(Y0), '.');  
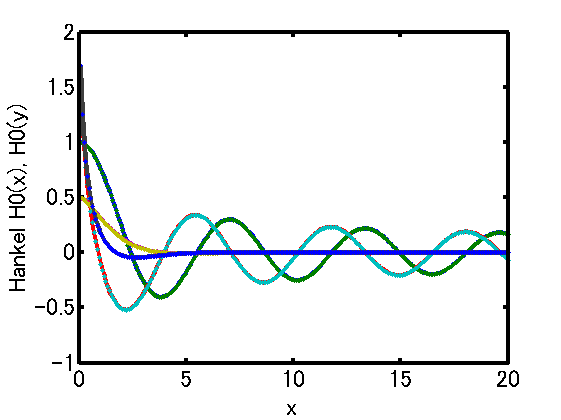
xlim([0 20]);
xlabel('x'); ylabel('Hankel H0(x), H0(y)');
print -dpng "hankel.png"
 
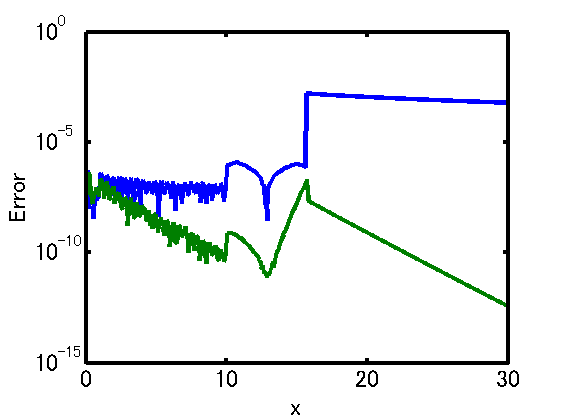
semilogy(x, ex0, x, ey0); xlim([0 30]);
xlabel('x'); ylabel('Error');
print -dpng "error.png"
 

結果

遠方の近似自体がそんなに精度良くないので精度を求めるときは使わないように。