ここではEuler Getterの数学的な側面を説明する。
もちろんゲームをプレイする分には理解しておく必要はない。
本家の説明は英語であるが大変分かりやすい。
盤面の取り決めついて
「点対称な位置にある縁のマスは同じマスと見なす。」
という Euler Getter の盤面の取り決めは、
盤面のトポロジーを(実)射影平面

にするための取り決めである。
ここでは、射影空間

について紹介する。
これは数学において大切な空間の1つである。
まず、「ユークリッド空間」について確認しておこう。
これは点や直線,平面といった普通の平らな空間のことである。
一般に

次元ユークリッド空間

を

個の実数の組の集合と定める。
私たちの住むこの空間も

という3つの実数の組と位置が対応しており、
3次元ユークリッド空間

だと見なすことが出来る。

次元ユークリッド空間

において
原点を通る直線の集合のことを

次元射影空間

と呼ぶ。
例えば、

はただの直線であるから、
原点を通る直線は1本しかない。
すなわち、

は1点である。
1つ次元を上げてみる。
平面

の中で原点を通る直線の集合が

である。
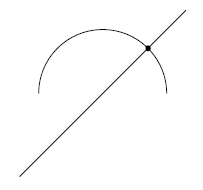
原点中心の円を考えると、このような直線が常にこの円上の2点を通ることが分かる。
したがって図のように半円上の点と直線が1対1で対応している。
境界の2点は同じ直線を定めるので同じ点だと見なせば、
結局

が円であることが分かる。
もう1 つ次元を上げてみる。
先と同様にユークリッド空間

内で
原点を通る直線は半球上の点と対応する。
ここで境界は対点が同一視された円である。
これが

であるが、この図形もまた球面になるだろうか?
試しに

のオイラー数を計算してみる。
オイラー数とは図形に対して定まる量で、例えば多面体の場合、
頂点の数 - 辺の数 + 面の数
を計算したもののことである。
通常の多面体について計算するとその値は常に 2 となる。
この事実をオイラーの多面体定理などと呼ぶが、
実は多面体とは球面をセル分割した図形であり、
2 というのは球面のオイラー数なのだ。
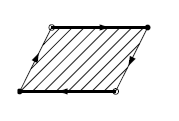
そこで下の図のように

もセルに分割し、
同一視に注意しながら頂点、辺、面の数の交代和を計算してみる。
答えは2 - 2 + 1 = 1 である。
様々なセル分割が同じ値1 を導くことを確認してほしい。
この計算は

が球面と異なる図形であることを示している。
こうして

が新しい図形であることが確認できたわけだが、
オイラー数が奇数であることはEuler Getter において重要である。
なぜなら2 人で

のオイラー数を取り合えば必ず勝負がつくからである。
このことがEuler Getter における盤面の取り決め
「点対称な位置にある縁のマスは同じマスと見なす。」
を採用する理由なのである。
決着について
偶数マスEuler Getterが先手必勝であること
2012年2月、数学者のChristian Schnellによって偶数マスEuler Getterが先手必勝であることが示された。
最終更新:2012年03月20日 10:22