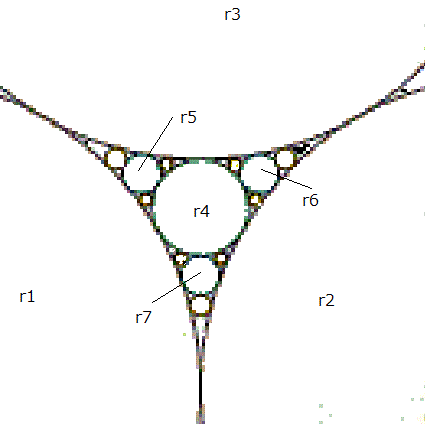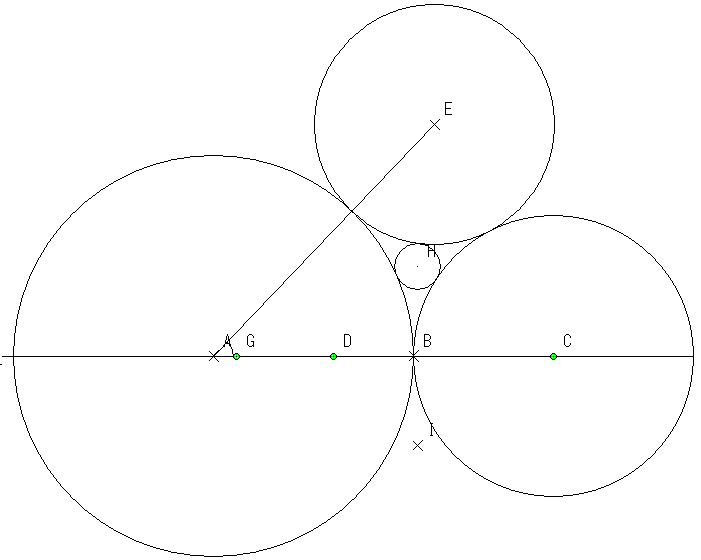Problem 199 「反復円充填」 †
問題
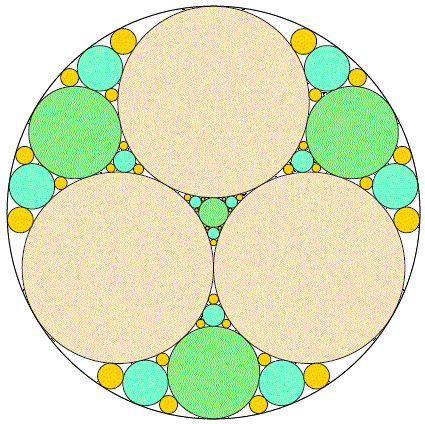
各ステップで, 全てのすき間にそれぞれ最大の円を置いていき, 結果として次のステップにはさらにすき間が増えていく. 3ステップ後には上の図のようになる. 108のすき間ができ, 円で埋められていない面積の比率は10進8桁に四捨五入して 0.06790342 となる.
10ステップ後に円で埋まっていない面積の比率はいくらか?
10進数8桁に四捨五入し, x.xxxxxxxx という形で回答を入力せよ.
用語定義
円のサイズ=円の半径や大きさと考えてください。
解法
まず答えの式を立てます。
(一番大きな円の面積-描かれる円の面積の合計)/一番大きな円の面積が答えなので、
計算するために描かれる円の面積の合計を考えてみます。
この問題は図をよく見て規則性を探すことで綺麗に解くことができます。
まず最初の3つの円の面積は幾何計算で簡単に求まります。
つぎにそれ以外の円の面積を求めましょう。
例として示された図を色分けしてみます。
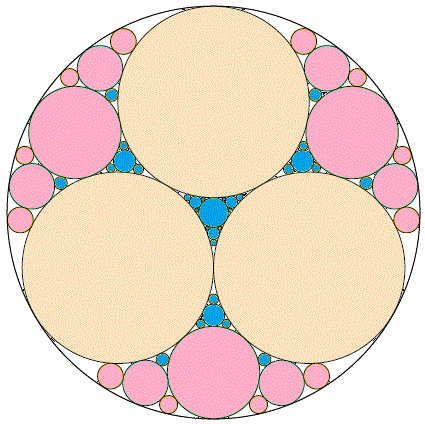
少し配色センスを疑われるかもしれませんがわかりやすさ重視で塗りました。
- A ピンクは一番大きな円に内接し、2つの互いに外接する円の間にその2つの円と外接する形で新しい小さな円が描かれています。
- B 水色は3つの互いに外接した円の間にそれら3つと外接する形でより小さな円が描かれています。
そして図は最初の3つの円を除きこの2種類しかなく、これ以後小さな円を派生(生成)させていっても2種類以外派生しません。
Aをoutな円。
Bをinな円とします。
outな円もinな円も3つの親となる円から生まれる(形や位置)が決定されることを確認してください。
次に生成される円の生成パターンを考えてみます。
outの円が描かれた場合そのoutから派生して描かれる円はoutな円がその左右に、円の中心方向にinな円が新しく派生します。
またinの円はinの円の周りに3つinな円が描かれます。
outな円の派生。
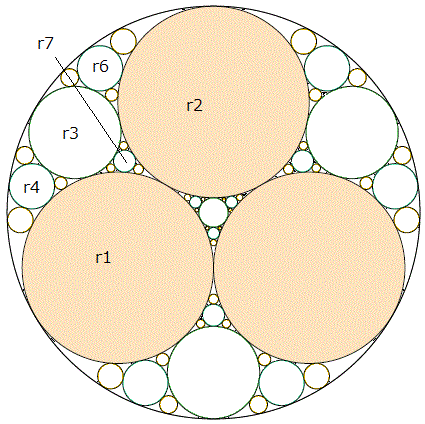
一番大きな円をR0としR1とR2の間にR3が描かれたとします。
R3から派生する円はR4、R6、R7となります。
次の円のサイズを計算する再帰関数を考えます。
実はoutな円もinな円も親となる3つの円のサイズだけから次の円のサイズが決まり座標は無視できます。(このことはあとで説明します)
3つの親となる円から周りの隙間に描かれる小さな円のサイズを決定する関数を
Ru=inR(Ri,Rj,Rk)
Ru=outR(Ri,Rj,Rk)
どちらも親となる3つの円のサイズを受け取りinRはinタイプの円をoutRはoutタイプの円のサイズを返す関数です。
ここの図では
R7=inR(R1,R2,R3)
R4=outR(R1,R2,R3)
R6=outR(R1,R3,R2)
と次の円のサイズが決定されます。
少し手順が前後しましたがR1,R2,R3の円が決定された場合、R3から派生する円は
R4=outR(R0,R1,R3)
R6=outR(R0,R3,R2)
R7=inR(R1,R2,R3)
と計算されます。
R3は円R0R1R2の3つからoutR(R0,R1,R2)と派生します。
R4やR6でもR3と同様の派生パターンを繰り返します。
R4の周りは
outR(R0,R1,R4)
outR(R0,R4,R3)
inR(R1,R4,R3)の3つの円が派生しますし。
R6の周りでは
outR(R0,R3,R6)
outR(R0,R6,R2)
inR(R2,R3,R6)
と円が派生していきます。
外周ではこの派生パターンが連続して続き、3つに分岐する単純な再帰関数で表現できます。
outRを一般化すると
Rk=outR(R0,Ri,Rj)
ならRkの周りで生成する円は
outR(R0,Ri,Rk)
outR(R0,Rk,Rj)
inR(Ri,Rj,Rk)
となりこの単純な漸化式がどこまでも続きます。
outRは一番外側の外周にできる円でinは内側にできる円です。
3つの円の間にできるinな円の派生
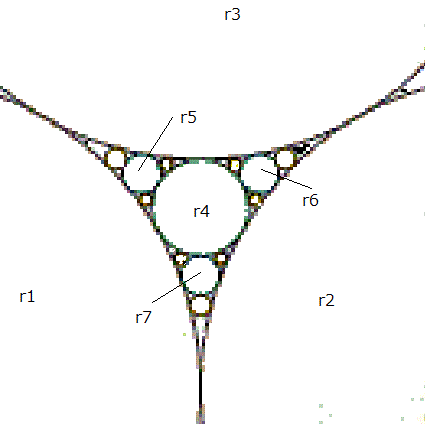
また3つの円に囲まれたinな円からの派生は。
(これは例なので円には適当な番号を割り振っています)
円R4は円R1,R2,R3から派生し。
円R4からは
R5=inR(R1,R4,R3)
R6=inR(R2,R4,R3)
R7=inR(R2,R1,R4)
と派生しこれ以後も同じパターンでより小さな円が派生します。
これも再帰関数で表現できます。
これによって全円の派生パターンを網羅したことになります。
小纏め
inな円からはinな円が3つ周りには派生して描かれ。
outな円からはoutな円が2つとinな円が一つ描かれることが判明し。
その規則性はとても単純で再帰関数で表現可能なことが判明しました。
描かれていくより小さな円のサイズの決定
次に描かれていく小さな円は親となる3つの円の半径だけから決まることを書いてみます。
inR関数を考えてみます。
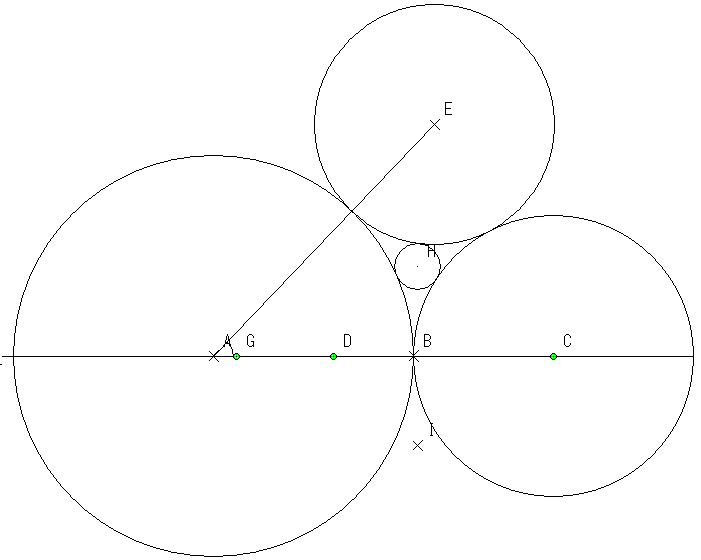
inRでは3つの外接する円の隙間に新しい円の半径が決定されます。
A,C,Eの3つの円の隙間に新しい円Hが派生する場合のHの半径を計算する方法を考えてみましょう。
計算しやすいよう
一つの円Aを原点にCをX軸にとるとEの位置を反時計回りな位置に決めると描かれる図は一意に決まります。
隙間に円Hが描かれますが、円Hはサイズが一意となります。
この図から派生する小さな円のサイズを計算するには大きな三つの円のサイズだけからいえることがわかります。
さてHを求める場合ですが
円ACEの座標円のサイズからHのサイズを決める3つの連立方程式を解けば答えが出てきます。
かなり複雑な式変形になるので式変形を自動でしてくれるソフトを使うとよいでしょう。
Hの周りに派生する3つの円も
inR(H,A,E)なら
- 点Hを原点にとりAをX軸にとれば次に派生する円のサイズが計算できます。
inR(H,A,C)も同様に
- 点Hを原点にとりAをX軸にとれば次に派生する円のサイズを計算できます。
inR(H,C,E)も
- 点Hを原点にとりCをX軸状にとれば次に派生する円のサイズを計算できます。
これ以後に派生するより小さな円も同じ手順でもとまります。
outな円もすこし計算方法や図が変わりますがinな円と同じ手法手順で順番に派生する円のサイズを計算できます。
纏め
ここまで判明したらあとは自力で考えられることと思います。
私の解説がよくわからなかった場合。
この問題は文章で考えるより図とよくにらめっこしたほうが直感的にわかるはずです。
なので図の意味をよく考えてください。
最終更新:2013年12月11日 12:52