Problem 164 「どの連続した3桁の和も与えられた数を超えない数」 †
解法
この問題は3桁から初めて1桁ずつ伸ばしていく動的計画法で解きます。
最初3桁で条件を満たす組み合わせをすべて元ます。
それに一桁ずつ足して4桁、5桁、、、の場合の組み合わせ数を計算し数字列と組み合わせ数のデータを20桁まで伸ばします。
伸ばすとき簡単な理由から末尾3桁で分類しながら組み合わせ数を計算すればよいのですが、それについて今から説明します。
最初頭3桁の数を考えます。
memo[10][10][10]の3次元配列を考えます。
memo[A][B][C]とします。
Aは1桁目の0~9の数字に
Bは2桁目の0~9の数字に
Cは3桁目の0~9の数字に
Dは4桁、、、
、、、
Tは20桁目の0~9
に対応します。
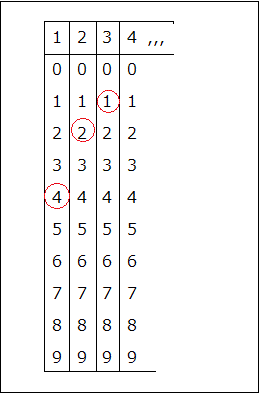
図のようなイメージですね。
図で3つ選択し、
A+B+C<=9かつA>0ならば
memo[A][B][C]=1
そうでないなら
memo[A][B][C]=0
を割り当てます。
memoの値は頭3桁の値がABCとなる組み合わせ数を現します。
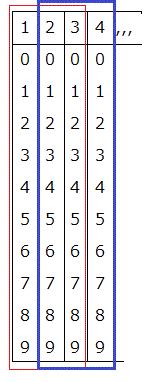
次に1~4桁目までの組み合わせ数を考えます。
次の段階を計算するための土台
next[B][C][D]を考え配列の中身は全部0で初期化(0クリア)します。
nextは4桁目の組み合わせ数を管理するためのデータです。
Dは4桁目の数です。
赤枠から青枠を求める作業を行います。
memo[A][B][C]が1かつ3桁の和が9以下になるという条件を満たしているもので、2~4桁目が条件を満たせばAの値は考慮することなくBCDの3種類の数だけで1~4桁目までの組み合わせ数を管理できます。
単純に1~4桁目までの組み合わせ数の管理は
ABCDは0000~9999まで全てためせばよく,4重ループで片が付きます。
4重ループの中でB+C+D=<9
ならAの値を考慮することなく4桁目の組み合わせ数を計算できます。
ループの中で
next[B][C][D]=next[B][C][D]+memo[A][B][C]
と足し合わせていけばよいと分かります。
難しく聞こえるかもしれませんが原理は単純です。
4桁はABCとBCDの連続した桁の和が9以下になればよくABCはmemoの時点で検証済みです。
よって4桁の組み合わせを管理するには4桁の末尾BCDだけで組み合わせの計算を管理すればよいと判明するわけです。
5桁を計算するときは4桁で末尾がBCDのものにEを追加するのですから、CDEが9以下を判断するためにCDに分けて組み合わせ数を記録するのが必須であると判明します。
nextの計算がすべて終わったらmemoの内容をnextで上書きします。
そしてnextを0クリアします。
-5桁目
3桁から4桁の組み合わせ数を求めた上記と同じことを行うと今度は5桁となります。
BCDからCDEを求めます。
BCDの組み合わせ数は3桁でABCが条件を満たし、BCDの3桁も条件を満たしたものだけがmemoに残っています、よって次もABを考慮することなくCDEだけで管理すればよいと分かります。
next[C][D][E]で5桁の場合の組み合わせ数を計算します。
計算法はBCDEを0000~9999までためし
C+D+E<=9となるものだけ
next[C][D][E]=next[C][D][E]+memo[B][C][E]
と計算すれば5桁目が出ます。
4桁の時と同様にnextの内容でmemoに上書きしnextを0クリアして。
あとは同じ要領で末尾3桁だけで組み合わせ数を管理しながら6ケタ~20桁の計算を行います。
最後にmemo[R][S][T]にできた組み合わせ数を集計すれば答えとなります。
蛇足
誰にとっても呼吸するように簡単にコードが欠ける問題というのがあると思います。
私にとってはこの問題はそういう問題でした。
そういう問題は自分にとってあまりにあたりまえに書けるために他人に伝えようとしたときどう伝えたらいいのかよくわからない状態です。
最終更新:2013年12月11日 12:48

