三角形の内部にある互いに外接する3つの等円に関する問題 - c21coterie @ ウィキ

ページ製作者　堀江　伸一
三角形ABCの内部にあり、互いに外接する3つの等円に関する問題の考察。

３円の中心をO1,O2,O3とする。
O1は辺ABと接し、O2は辺ＢＣと接し、O3は辺ACと接するとする。

任意の三角形が与えられたとき、O1の解集合を求めよ。

只今考察中。
ネットでたまに見かける、高校の先生が初等幾何の問題を自分なりに解いてみました。
というあれに近い感じでまとめられたらいいのだけど。
まずは作図。

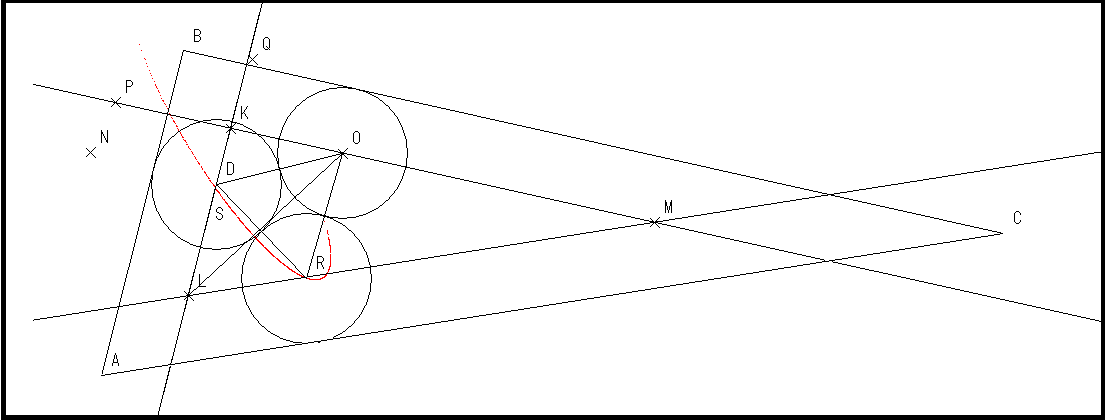
作図ソフトで眺めていると、デカルトの葉線が赤線として見えている。
これは結構難しい、2次曲線は初等幾何でおなじみの曲線だから楽。
葉線についてきちんと扱った本を読んだことがないので性質がよくわからないのが難しい所。
このへんは微積分で一般的にアプローチすればいいかな？
この問題幅aだけ辺を平行移動して三角形の辺を縮めた三角形上に特定の正三角形が描けるかという問題になる。

機械的に答えが出る方法は以下の通り。

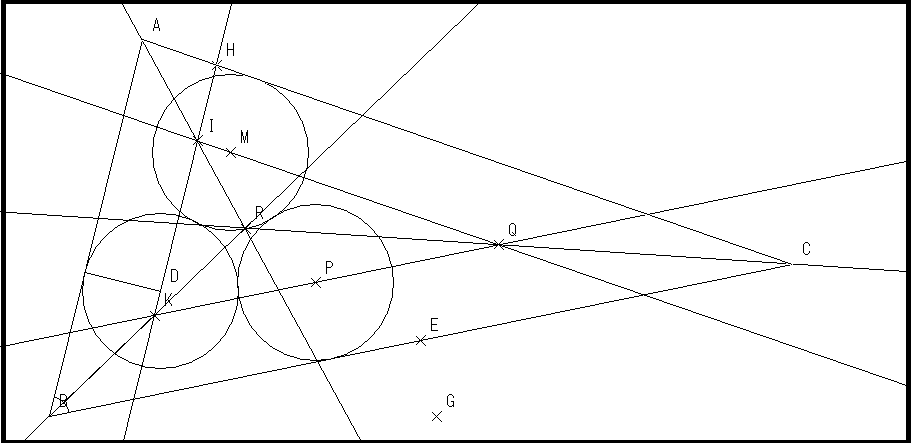
三角形ABCの内心をRとしこれを原点とします。
実数0<s,k,t,r<1を考えｓを定数として確定します。

s→RAとABの距離をLとします。
→RD=sk→RA+s(1-k)→RB
→RP=st→RB+s(1-t)→RC
→RM=sr→RB+s(1-r)→RA
から
4L^2=|DP|^2=|PM|^2=|MD|^2を考え。
この式を整理して2次方程式の解の公式よりｔ、ｒをｋで表します。
後はｋを解けば答えとなりますが式変形がめんどくさすぎます。
またｓをX軸にｓに対し定まるｋ　ｔ　ｒをｙ軸に表記してグラフを見れば
性質が見えてくる思いますがこれを行うには少し高度な数学ソフトが必要そうです。

また三角形の形が代わるたびに答えが代わりますから、三角形の形と解の関係に対する統一的な見解に至るにはもう少し高度な発想が必要が必要なようです。

そこで少しでもこの問題の性質を見極めるために発想を変えてみます。
三角形KIQはｓの値によってサイズが代わりますが、3つの辺の上に円の中心D,M,Pをとって描ける正三角形の数はサイズによらず決まっています。
三角形ABCが正三角形でなければ描ける正三角形は数えられる有限個しかないはずです多分。
そして、描けた正三角形のサイズはｓに比例して大きくなり、距離Lはｓに比例して小さくなります。
よって描けた正三角形のサイズとLが同じになる場所が答えとなるはずです。
つまり正三角形を除く一般の三角形ABCでは答えとなる円の中心は有限個の点となる可能性が高くなります。