名前 堀江伸一
2010/5/20~21日

自作の水彩画フィルタ。
右がフィルター後で左がフィルター前。
近傍点に対するフィルタ処理という概念を拡張して作った。
基本的な処理は簡単。
まずは元絵と、元絵と同じサイズの白紙の絵を用意し、白紙のほうをフィルタ絵と呼ぶ。
元絵を升目で区切ってその升目の中に似た色が多ければ、白紙の絵の同じ座標に塗りつぶし半透明の設定で円を描く。
そして全ての升目をチェックして同じように円を描いていく。
チェックが終わったら升目を小さくして、同じ円を描く処理を繰りかえしていけば、最後には円で絵を近似でき左の写真より右の水彩画風イラストが完成すると言う寸法。
上記処理だけだと元絵の細かい部分が失われやすいようです。
防ぐためにサイズの大きい円を描くまえに、元絵を円形に切り取りこれを半透明にしてからフィルタ絵のほうに敷き、その上に円を描く処理を行ってみました。
料理と一緒なので隠し味や調理法はお好みで。
円を描く確率を下げ、水彩画風のぼんやりとした色合いの円を描く風にプログラムを描き直すと、アニメ塗りを水彩画風に直せるようです。
この手法の問題は、基本的なフィルタ処理との違い。
全ての点の近傍点に行列をかけて、処理後の点の状態を決定するという最もシンプルなフィルタ処理と違いが出ているかどうかという点?
僕のほうの水彩画フィルタはサイズの違う行列の組あわせが各点に対して複雑に適用されます。
各点に対して適用される行列のサイズと形が絵によって動的に変わると言ってよいわけ。
この処理、処理的にいえばニューラルネットワークの簡素版とも言える。
この処理の改良案もあります
- 白紙の紙に円が描かれるとき、円がもう塗られたところに上塗りするならどのように上塗りするか、その塗り方をニューラルネットワークの重み付けで近似したい。
- 絵を円以外の方法で近似する手法を模索したい。
- 円以外の形を遺伝的プログラムで決定したい、升目の状態に応じてどのような形を白紙のほうに塗るか、それを決定するための条件分岐付木を作りたい。
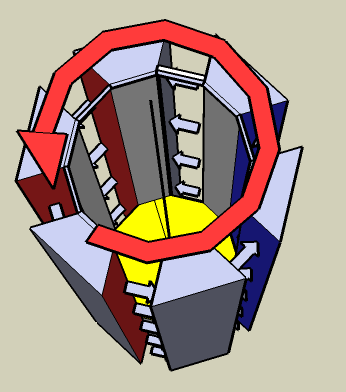
ウィキバーシティに投稿した作図、GNU3.0ライセンス 作図者 堀江伸一
コンデンサガン。
コイルガンの亜種。
コイルガンは、砲身の周りにぐるぐる巻きにされたコイルの中を電子が走ることで磁力を発生させて弾を発射する。
では、なぜコイルなのか?
電子が砲身の周りを回るなら、コイル外の何でもいいのではないかと考えて作図してみた。
赤い板と青い板はコンデンサをあらわす。
振幅コンデンサの間を電子が移動しているとする。
この状態で砲身を高速回転させると、コンデンサの間を行き来する電子が砲身と同じ方向に回転するときは板に中々おいつけず電子の速度が上がり、砲身と逆向きに電子が動くとすぐに反対側のコンデンサの板に当たる。
よって全体としては、電子が砲身と同じ方向に高速回転することになる、、、はず。
だれかご意見待ってます。
本屋で理系への数学3月号を受け取る。
ストックがないと聞いていた2月号、1月号も手に入った。
紀伊国屋凄い。
アマゾンで買ったら2000円以上取られるところを定価で買えた。
早速ぱらぱら読み。
3体問題と「部分と全体」の300年というコラムが面白い。
系の中の要素、各要素間の相互作用の平均数がeを超えたら、系が複雑系になる確立が急速に上がり、これは広範な系似適用できる。
と言う話。
ちょっと大言壮語なきもするが面白い。
このeという数字を頭の片隅に置きながら、同誌掲載のコラム、パラドックスの科学を読むとちょっと面白い。
意思決定のパラドックスを取り上げている連載のようだが、これも意思決定にかんする相互作用がeを超えたからパラドックスが生まれているのかもしれない。
ほかは普通に読む。
この雑誌は、チャート式で数学ⅢCをやり終えた後の人ぐらい向けかな。
なんとなく、難しすぎず簡単すぎずいい雑誌。
難しいのはなんとなくそんなものかと読んで、やさしいのは分分といいながら読む。
各コラムが短いので時折取り出してぱらぱらと読んで、ちょっと考えて終わるには調度いい長さ。
一年2年と付き合っているうちに、地層に泥が堆積するように、なんとなく数学分野が頭に堆積するようなイメージだ。
入門にはいい雑誌だと思う。
2010/5/20
最近どうも頭の調子が悪い。
小説を書ける気もしない。
けど、本当に凄いのはリンク先の人が通っている学校RSS暗号の原理とかを中学生で学ぶらしい。
こっちなんか、普通の高校数学の教科書1年より難しい授業受けたことがないのだが、
RSSとか、素因数分解に連なる難しい問題だよな。
普通の学校なら高校数学やり終えた後に数学好きが手を出すレベル?
なんてのかな、スタートから違うと思う。
こういう環境で生きていると、チャンスが目の前に来たとき飛びつく能力が高いんだろうな。
それにこういう有利な環境で生きているとチャンスのほうから勝手にやってくるんだろう。
受け答えもしっかりしているし。
人間人生におけるチャンスの回数と、チャンスについていける能力。
これって平等じゃないんだ。
普段からチャンスの回数が増えるように生きてないと駄目なんだろう。
昔ITで誰にでも大金をつかめるチャンスが。
というのがやたらと宣伝された時期があったが。
過ぎてみれば、チャンスを物にしていたのはエリート中心だった。
どこにでもいる大学生がIT技術と誰にでもかけるプログラムで大金を、というのはよく調べると引く手あまたのMITのエリート大学生だった。
どこにでもいる一社員がIT会社を立ち上げて荒稼ぎは、もともと何年も前からその分野に携わっている専門家で人脈を多数持っていた。
IT技術の旗手と騒がれた人間はもともとカリスマの持ち主だった。
でも、そういう人間にくっついてバブルの泡の上に載った連中もいたわけだが、そいつらはラックか目ざとさが会ったのだろう。
誰にでもチャンスなんてのは馬鹿を躍らせるための宣伝だったんだろうか。
凡人に出来るのは地道な努力と、チャンスを探す能力を鍛えることしかないのだろうか?
でもポストドクになることもあるから、世の中難しい。
集合論のレベルから2次元にカオス系が生まれる部分の解説を読む。
感覚的には分かったが、理屈をきちっと紹介しろと言われたら困るレベルで理解。
あれ、記号でやるからメンドクサクて難しそうに見えるだけで、子供に粉入り容器を持たせて、容器から容器へ粉を移す過程と捉えれば、カオス系の本質が中学生でも分かるわけだ。
粉は移されるたびに、容器の中でn倍に分裂して溢れる粉と溢れない粉が生まれる見たいな。
本屋に理系への数学3月号をちょっと受け取りに行こう。
2010/5/19
今日は家族が個人譲歩王を全部消せと言うので消去して回る。
編集履歴30回越えで履歴が消えそうなアイディアもあるのでちょっとひやひや物。
340あるページのうち250くらいあるネームだが、保存用にと重複するネームも多かったのが幸い?
重装型炎鬼の槍のアイディアはずっと掲載するの忘れていたな。
掲載していた気になっていただけだったのをいまさら掲載。
すると炎鬼のアイディアは相当前にTwitterでつぶやいた分が最古と言うことになってしまう。
Twitterで”今日”という単語を検索して眺めていると楽しい。
皆色々なことをやっているんだな。
文法の違いが面白い。
ラジオツイッターでないかな。
高性能ボイスチャットでつぶやかれたつぶやきがラジオみたいに流れるとか。
ほかに、勝手に読み上げてくれるとか。
画面を長時間見るのめんどくさい。
でも今日という単語で検索するのはかなり楽しい。
Twitterの無関係な文章を組み合わせて勝手に会話を成立させる遊びとか?
Twitterで無差別コメントでもやってみようかな。
わかっている、自分が痛い人だって分かっているけど、まあ一種の病気である。
2010/5/18
今日は原付が家に来る日。
ヘルメットは購入済みだし。
原付きたー。
結構楽しかった。
最初お店の人が家まで持ってきてくれて乗り方まで親切に付き合って教えてくれたし。
乗ってみたら簡単。
初めての自転車よりは早く乗れた。
風が気持ちよかったので、一人で北のほうに走って今日の走行距離は30km。
交差点で曲がるとき要注意。
どうしても曲がれないときは、車がいなくなってから曲がる。
意外と速度がでないのが原付かな。
車と違って風や音がダイレクトなのが楽しい。
後猫みたいに隙間を好きに走れるし。
後はとりあえず今日はハードSF用設定コンデンサコイルガンの作図もやっとこ。
2010/5/17
今話題の口蹄疫のウイルスイラスト、正12面体をしているのね。
ウイルス表面をなす化学物質を選んで面か頂点の周りをつくり、それらを結合していくとウイルス表面になるのかな何てことを考えてしまう?
最初に正12面体を作った人はこんな世界に12面体があるなんて考えもしなかったに違いない?
それにしても今回の伝染病騒ぎはやたらと農水省の無策が取り上げられているようだ。
最終更新:2010年05月21日 16:59

